Un graphe est constitué par un ensemble d'objets (représenté par des sommets) reliés entre eux par des liens (les arrêtes du graphes).

Un graphe permet de représenter le réseau ferroviaire, le réseau internet, un labyrinthe ou certains problèmes de choix de chemins.

I)L'EXEMPLE DU BERGER

Le problème : Un berger près d'une rivière possède une chèvre, un chou et un loup. Le berger doit faire passer un a un ces 3 derniers de l'autre côté de la rivière par barque.

CONDITIONS:

-Sans berger :

*chèvre et loup seuls = le loup mange la chèvre

*chou et chèvre seuls = la chèvre mange le chou

-En présence du berger : personne ne mange

t=0 tfinal

RIVE ARRIVÉE rien B + L + C + Cx

___________________________________________________________

RIVIÈRE

___________________________________________________________

RIVE DÉPART Berger+Loup+Chèvre+Choux rien

B + L + C + Cx

IL y a 16 situations possibles. Chaque état sera simplement écrit grâce au personnages présents sur la rive de départ.

LISTE DES ÉTATS INTERDITS :

L/C

C/Cx

B/Cx

B/L

(4 situations interdites)

SOLUTION:

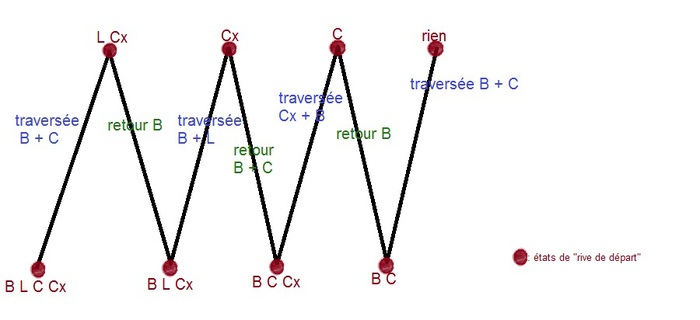
II)COMMENT SORTIR D'UN LABYRINTHE ?

Les intersections sont les sommets du graphe et sont repérées par des lettres. Les couloirs sont les arrêtes.

Parcours en largeur :

1- A

2- AB

3- ABC

ABM

4- ABCD

ABCK

ABM (On ne peut prolonger qu'1 seul point en même temps dans une étape)

5- ABCD

ABCK

ABMN Impasse

ABMZ // solution

Le parcours en largeur permet de trouver le chemin le plus court pour sortir du labyrinthe.

Parcours en profondeur :

1- A

2- AB

3- ABC

ABM

4- ABCD

ABCK

ABM (On ne peut prolonger qu'1 seul point en même temps dans une étape)

5- ABCDE

ABCDK éliminé car K est reutilisé

ABCK

ABM

6- ABCDEF éliminé car Impasse

ABCDEG

ABCK

ABM

7- ABCDEGH éliminé car Impasse

ABCDEGI

ABCK

ABM

8- ABCDEGIJ éliminé car Impasse

ABCK

ABM

9- ABCKD éliminé car comme on l'a vu avant il va y avoir que des impasses après

ADCKL éliminé car Impasse

ABM

10-ABMN éliminé car Impasse

ABMZ